Expanding from Weierstrass To General Form

Taking the Weierstrass form of an Elliptic Curve, and translating our x-values and y-values, with functions, we can convert the Weierstrass form of an Elliptic Curve to a more general form (related to but slightly extending the equation defined in - Washington, L. C., 2008, p10, Equation 2.1). The resulting curve is still an elliptic curve.

IMPORTANT: this more general form of the elliptic curve is not generally symmetrical around the x-axis. As such, the calculation of the additive inverse becomes less straightforward. This will be explored more, in other sections.

However, as we explore in more detail below, we can show that these specific translations at no point cause the additive inverse (P and P' = -P ) to be other than vertically in line with with each other.

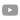
Take the Weierstrass form of an equation for an elliptic curve:

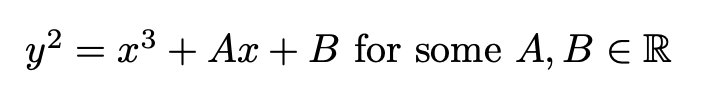
Now translate both x-values, and y-values through the following functions:

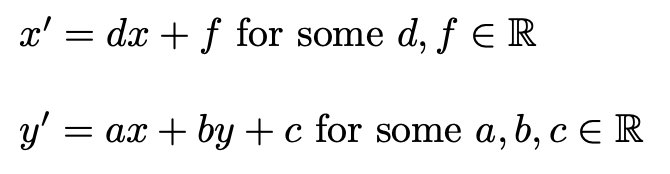
We get a new equation for the elliptic curve - which is:

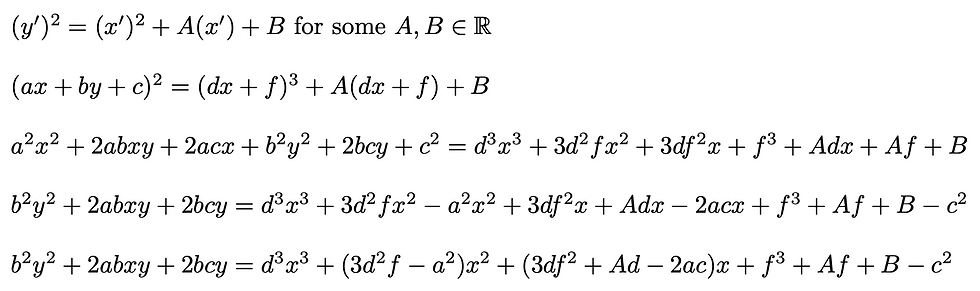
Which is of the form:

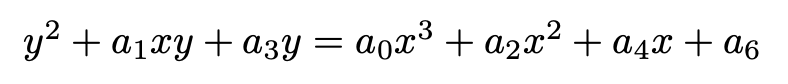
Where:

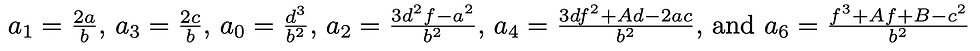
The equation:

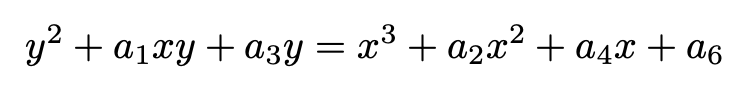
is commonly recognised as the general form of an elliptic curve, sometimes called the "generalised Weierstrass equation" of an elliptic curve (Washington, L. C., 2008, p. 10, Equation 2.1), which is the same as the form of the equation derived above, except for the addition of an x^3 coefficient, a_0. The removal of this coefficient is attainable, by dividing the right-hand side of the equation through by a_0 = (d^3 / b^2). Doing so would leave the graph of the equation (imagining this defined in the field of the Real numbers) compressed in a vertical direction towards the x-axis, but otherwise topologically unchanged. In other words, the form of the equation derived above, and the "generalised Weierstrass equation" described in Washington are isomorphic.

This gives a indication as to how we might reliably transform an elliptic curve in the general form back into the more specific Weierstrass form.

Adding these transformations, step-by-step

The inclusion of each of the values:

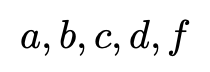
in the equations:

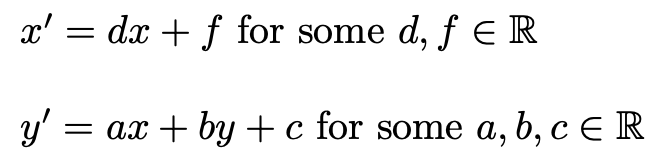
transform the equation in ways that can be easily understood visually, when defined in the field of Real numbers, and graphed on a 2-dimensional plane.

First imagine we only alter the value for d - that is:

We see that the elliptic curve is squeezed and stretched, in the horizontal direction.

Then imagine we only alter the value for f - that is:

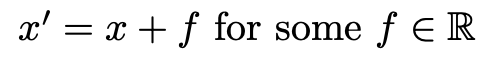
We see that the elliptic curve slides from side to side, in the horizontal direction.

And when we alter both at the same time - that is:

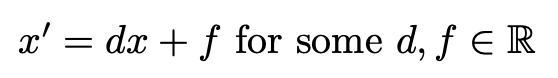
We now introduce a faint dotted grid to these animations, to assist with the visualisation of what is happening to the space across which the elliptic curve is defined.

Imagine we only alter the value for b - that is:

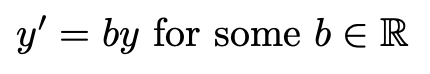
and we see that the elliptic curve is squeezed and stretched, in a vertical direction.

Then imagine we only alter the value for c - that is:

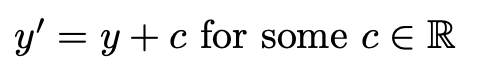
We see that the elliptic curve slides up and down, in a vertical direction.

Then imagine we only alter the value for a (this is one of the most interesting translations) - that is:

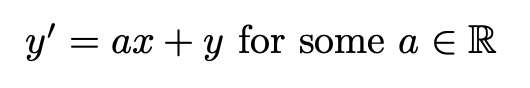
We see that the elliptic curve slides up and down, relative to how far away from the y-axis each point is. That is, at x = 0 nothing changes, but as you move further away from the y-axis the effect of the “vertical sliding” gets greater... creating parallelograms where there were once squares (watch the green grid points in the graph).

In each of the separate translations animated above, we see that all points that are vertical to each other in the original graph, remain vertical to each other in the translated graph. This is important for our further understanding of the additive inverse, and how it is effected by these translations. This concept will be explored further in the next section.

Finally, we see the behaviour of the curve when all 5 values are changed at the same time. Pay close attention to the line between R and R′ = −R = (P+Q), and the fact that it remains vertical the whole time.