Arithmetic in a Finite field
- Nicholas Gledhill
- Mar 26, 2024
- 6 min read
Updated: Jun 3, 2024
The operations of adding and doubling points on elliptic curves defined over finite fields form the cornerstone of elliptic curve cryptography (ECC), a key area of modern cryptographic systems. These operations are not only mathematically interesting but also critical for ensuring secure digital communications, encryption, and digital signatures.
Below we will investigate some of the calculations involved in doubling points in a finite field - the Formal Derivative and division in a finite field (the multiplicative inverse). Finally, we will investigate the process of adding points in a finite field.

Importance in Cryptography
Efficiency and Security
Finite Field Operations: When elliptic curves are defined over finite fields (Washington, L. C., 2008, pp95-142, Chapter 4) (such as Fp where p is a prime number), the group operations (addition and doubling of points) are discrete and cyclic. This discreteness provides a controlled environment conducive to defining hard problems such the Elliptic Curve Discrete Logarithm Problem (ECDLP) (Washington, L. C., 2008, pp143-168, Chapter 5), which is computationally infeasible to solve efficiently with current technology and forms the basis of security in ECC
Hard Problems: The security of ECC relies on the difficulty of reversing these group operations, particularly the ECDLP, where given two points P and Q on the curve, finding an integer k such that Q = kP (i.e., P added to itself k times) is computationally hard.
Practical Application
Digital Signatures and Key Exchange: Operations such as point addition and doubling are fundamental for algorithms like ECDSA (Elliptic Curve Digital Signature Algorithm) (Washington, L. C., 2008, pp179-180, Section 6.6)and ECDH (Elliptic Curve Diffie-Hellman) (Washington, L. C., 2008, pp170-173, Section 6.2). These protocols utilise the properties of elliptic curves over finite fields to create secure digital signatures and facilitate secure key exchange mechanisms, respectively.
Differences from Real Fields
Closure and Finite Nature
Finite Fields: In finite fields, the values of the points and coefficients are taken modulo a prime p ensuring that all possible results of point operations remain within a finite set of values. This provides the necessary closure and finiteness that is ideal for digital systems, which inherently rely on finite data representations.
Real Fields: In contrast, operations in real fields involve continuous values and do not naturally lend themselves to the modular arithmetic crucial for defining and securing cryptographic operations. Real numbers lead to issues with precision and practical implementation in digital systems due to their infinite decimal expansions.
Visualisation and Computation

Discrete vs. Continuous: Points on elliptic curves over real numbers can be visualised (below) as smooth continuous curves, making them great for theoretical analysis and understanding. However, elliptic curves over finite fields look quite different (left); they consist of discrete points which do not form a continuous line, aligning better with digital computation that requires discrete steps and finite states.

Predictability and Security: The predictable nature of real number operations (and specifically, relatively simple reversibility of operations) can be a drawback in security contexts, where unpredictability and hardness of problem-solving are crucial. Finite fields introduce a level of unpredictability, and irreversibility essential for cryptographic security.
This is analogous to the difficulty / irreversibility of the factorisation of the product of two large prime numbers, in the RSA encryption process. Both problems rely on the mathematical difficulty of reversing a process that is computationally easy to perform but hard to invert.
The Process - an example
Take a specific elliptic curve, say:

modulus 13.
Find all the integer values of x and y for which the equation of the elliptic curve holds true. These points are not always as obvious, intuitively - or as easy to calculate - as they are for the elliptic curve defined in the field of Real numbers.
For example, when y = 11, and x = 4:

and:

However, when taken modulus 13:
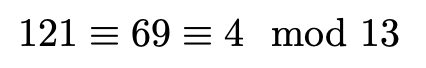
And so (4, 11) is a solution to the equations, i.e. a point on the elliptic curve.
NOTE: because of the symmetrical nature of the curve, if (x, y) is on the curve, so is (x, -y) = (x, p-y) mod p. And so we know immediately that (4, -11) = (4, p-11) = (4, 2) mod 13 is on the curve - which can be confirmed by calculating: 2^2 = 4.
The list of points on this elliptic curve is:
(0, 1), (0, 12), (1, 4), (1, 9), (4, 2), (4, 11), (5, 1), (5, 12),
(7, 0), (8, 1), (8, 12), (10, 6), (10, 7), (11, 2), (11, 11), (12, 5), (12, 8)
As seen graphed here:

Arithmetic on an Elliptic Curve in a Finite Field
In a finite field, the "gradient" can be found by the same method as for an elliptic curve in the field of real numbers - however: we must invoke the concept of the Formal Derivative, to do so rigorously, as finite fields are without a concept of a limit (or the concept of "approaching" a value, in infinitesimally small steps), upon which to define the idea of finding a slope, as two points become one.
Furthermore, the concept of "division" must be altered. All division, in these calculations, must be done in a way that adheres to the process of division for modular arithmetic.
In modular arithmetic, we focus on the fact that division should "undo multiplication" (see: Section 2.1 of this publication). This is achieved by multiplying the dividend by the modular multiplicative inverse of the divisor. We know that the modular inverse must exist, because the elliptic curve is defined on a field - and all values in a field have a modular (multiplicative) inverse.
First, we find the equation for the slope of the tangent to the curve. That is:


this would mean:

Substituting in the values for the point we used before, (4, 11), we get:

But (and this is the important part, with reference to division, in a finite field), in order to divide by 9, you multiply by its (9's) modular multiplicative inverse. The modular multiplicative inverse of 9 is the number, in the field, which when multiplied by 9 is equivalent to: 1 mod 13.
To work out the modular multiplicative inverse of 9 mod 13, we can use a few different approaches. In this case, we will use Fermat's Little Theorem. That is:

that is, the modular multiplicative inverse of 9 mod 13 is 3.
So now we can calculate the integer (mod 13 ) value for dy/dx - that is:

and so, the gradient of the tangent of:

at the point (4, 11), is 4. Leading us to conclude that the tangent line to the curve that passes through (4, 11) has the equation:

This line y = 4x + 8 is:
tangent to the curve y^2 = x^3 + x + 1 at P = (4, 11)
guaranteed to pass through one other point on the curve (see previous calculations)
will ONLY pass through ONE other point on the curve (see the fact that a line, passing through more than 2 points on (or that is tangent to) an elliptic curve describes a cubic, and therefore has a maximum of three solutions, in previous calculations)
NOTE: we take the point that it crosses to be:
R = -2P
and its point of reflection (mod p) is:
-R = (x_r, -y_r) = (x_r, p-y_r) = 2P
and so, we have found the position of 2P.
Visualising the tangent to the Curve in the Finite Field
Following is an animation, that helps to visualise the behaviour of the tangent to an elliptic curve:

in as finite field (modulus 13).
By drawing a tangent line from our "point of interest, on the curve", we see the following:
Note:
the point we are doubling, at P = (4, 11)
the line coming from it, at a slope of 4, traversing the space between 0 <= x < 13, and 0 <= y < 13
the fact that, like the physics of the 80s game Asteroids, when the line reaches a border of the space, it re-enters the space, on the opposite side of the space, at the same gradient (NOTE: the idea to visualise the tangent line as a line that crosses the border of the space, and back in the other side was taken from here: "A (relatively easy to understand) primer on elliptic curve cryptography".
the points R = (8, 1), and 2P = (8, 12), and the vertical line joining them, appear as the tangent crosses the point R, because this indicates that 2P + R = the point at infinity and that the additive inverse of R is 2P
the tangent line eventually crosses the y-axis at y = 8 - as clear from the equation y = 4x + 8
the tangent line continues through the space and eventually ends up back at P, having passed through the top/bottom of the space 4 times (the same as the value of the tangent slope). NOTE: it is necessary that the tangent line eventually meet P again, after m number of vertical transitions through the top/bottom of the space, as it also does not matter which direction from P the tangent line is drawn. It will always pass through P.
To show that the point at which the tangent line intersects with the curve again is the right point, see the following:

which shows that the three points of intersection of the curve and the tangent line at P = (4, 11) are:
x = 4 (twice), and
x = 8
Putting x = 8 back into the equation for the tangent line, we get:

which further shows that the other point of intersection between the tangent line and the curve is:
R = (8, 1)
as shown in the animation above.





















